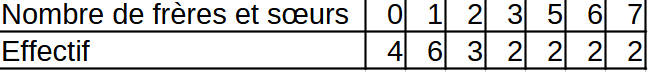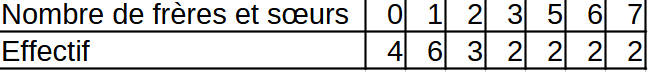Chapitre 16 : Statistiques

Définition :
On appelle série statistique le résultat d’une étude menée sur une certaine population, visant à mesurer la présence d’un certain caractère au sein de cette population.
Exemple :
La série statistique correspondant au nombre de frères et soeurs des élèves de 4C est :
5 ; 0 ; 2 ; 1 ; 1 ; 7 ; 2 ; 0 ; 1 ; 7 ; 6 ; 0 ; 3 ; 1 ; 3 ; 2 ; 0 ; 5 ; 6 ; 1 ; 1 .
L'effectif total est de 21 personnes.
Définition :
Pour calculer la moyenne, on additionne toutes les valeurs, puis on divise par le nombre de valeurs.
Exemple :
La moyenne de frère et soeur est de 5+0+2+1+1+7+2+0+1+7+6+0+3+1+3+2+0+5+6+1+121=5421≈2,57
Définition :
La médiane d'une série statistique est la valeur du caractère qui partage la population en deux effectifs égaux.
Méthode :
Pour trouver une médiane, il faut trier les valeurs dans l'ordre croissant. On note N l'effectif total
Si l'effectif total est impaire, la médiane est le N+12ème élément.
Si l'effectif total est paire, la médiane est la moyenne entre le N2ème élément et le N+22ème élément.
Exemple :
Voici la série triée dans l'ordre croissant : 0 0 0 0 1 1 1 1 1 1 2 2 2 3 3 5 5 6 6 7 7
L'effectif total est de 21 (donc impaire), donc la médiane est le 21+12=11 donc la médiane est 2.

Si on ajoute monsieur Garcia, la série dans l'ordre croissant devient 0 0 0 0 1 1 1 1 1 1 2 2 2 3 3 5 5 5 6 6 7 7.
L'effectif total est de 22 (donc paire), donc la médiane est la moyenne du 222=11ème élément et du 22+22=12ème élément donc la moyenne entre 2 et 2 est de 2+22=2 donc la médiane est de 2.
Méthode :
On peut calculer une moyenne à partir d'un tableau : 0×4+1×6+2×3+3×2+5×2+6×2+7×221=5421≈2,57