Chapitre 15 : Solides
Définition :
Un polyèdre est un solide délimité par des polygones appelés faces. Les côtés de ces polygones sont appelés arrêtes, et les points sont appelés les sommets.
Un polyèdre est un solide délimité par des polygones appelés faces. Les côtés de ces polygones sont appelés arrêtes, et les points sont appelés les sommets.
Propriété :
En perspective cavalière, les arrêtes parallèles sont représentées parallèlement et les arrêtes cachées sont pointillées. Les arrêtes fuyantes sont rapetissées.
Définition :
Un pavé droit (aussi appelé parallélépipède rectangle) est un solide à 6 faces rectangulaires telles que les faces opposées soient parallèles et de même mesure, et telles que les arrêtes adjacentes soient perpendiculaires. 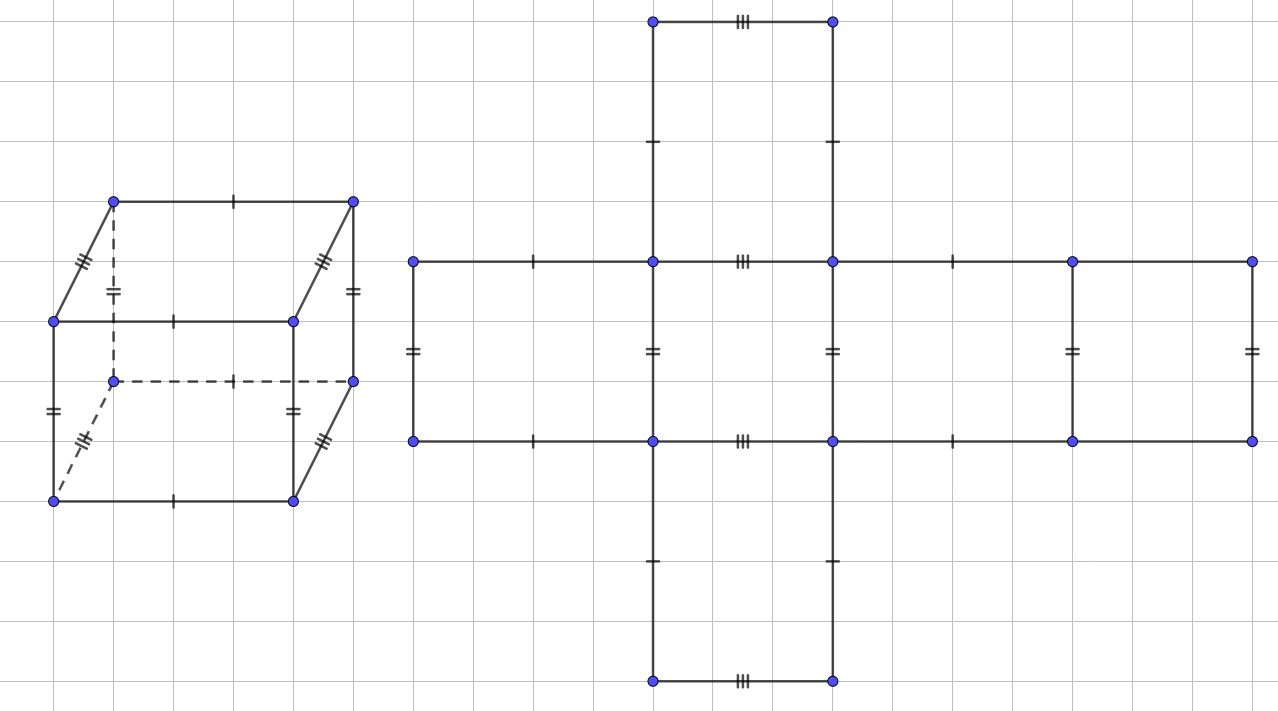

Définition :
Un cube est un pavé droit dont les faces sont carrées.
Définition :
Un prisme droit est un polyèdre qui a : 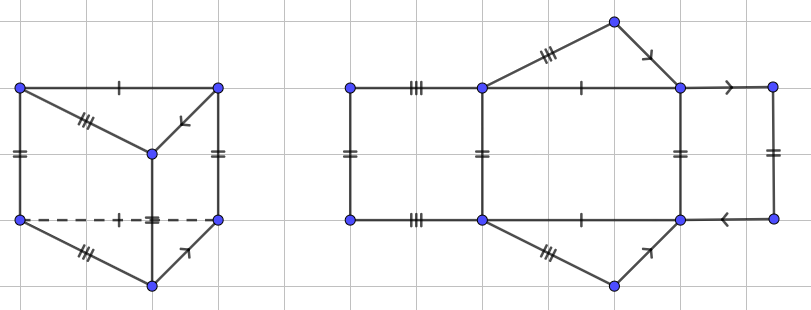
- Deux faces polygonales superposables et parallèles appelées bases
- Des faces rectangulaires appelées faces latérales

Définition :
Un cylindre est un solide qui a comme base deux disques parallèles et superposables tel que le segment d'extrémités les centres des deux disques soit perpendiculaire aux rayons de ces disques.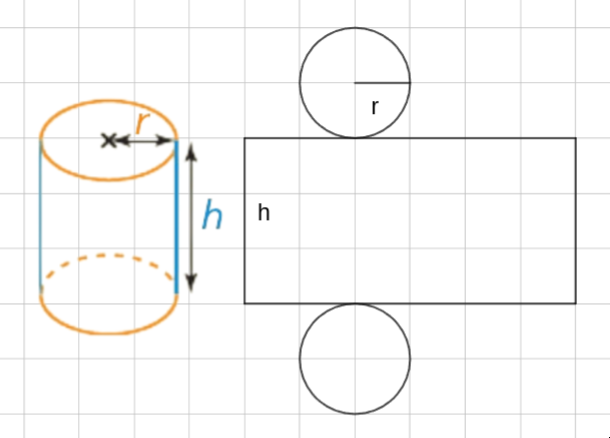

Propriété :
Le volume d'un pavé droit est égal à
Le volume d'un cube est
Le volume d'un cube est
Exemple :
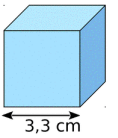 Le volume du cube ci-dessus est de
Le volume du cube ci-dessus est de
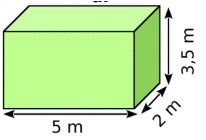 Le volume du pavé droit ci-dessus est de
Le volume du pavé droit ci-dessus est de
 Le volume du cube ci-dessus est de
Le volume du cube ci-dessus est de  Le volume du pavé droit ci-dessus est de
Le volume du pavé droit ci-dessus est de
Propriété :
La longueur de la hauteur d'un prisme droit ou d'un cylindre est la distance entre ses deux bases.
Le volume d'un prisme droit est égal à
Le volume d'un cylindre est
Le volume d'un prisme droit est égal à
Le volume d'un cylindre est
Exemple :
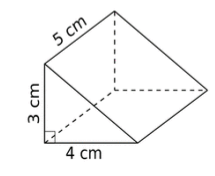 La base de ce prisme est un triangle rectangle. Donc l'aire de ce triangle est
La base de ce prisme est un triangle rectangle. Donc l'aire de ce triangle est
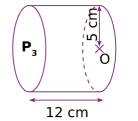 Le volume de ce cylindre est de
Le volume de ce cylindre est de
 La base de ce prisme est un triangle rectangle. Donc l'aire de ce triangle est
La base de ce prisme est un triangle rectangle. Donc l'aire de ce triangle est  Le volume de ce cylindre est de
Le volume de ce cylindre est de