Chapitre 13 : Transformations
Activité 1 :
Indiquer si les figures suivantes admettent un centre de symétrie et des axes de symétrie.
Exercice 1 :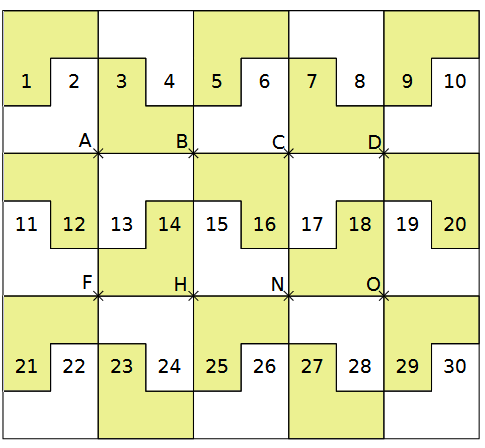 
a. Dans la translation qui transforme A en H :
• quelle est l’image de la pièce n°13 ?
• quelle est l’image de la pièce n°6 ?
• quelle est l’image de la pièce n°15 ?
• quelle est l’image de la pièce n°1 ?
b. Dans la translation qui transforme H en A :
• quelle est l’image de la pièce n°25 ?
• quelle est l’image de la pièce n°18 ?
• quelle est l’image de la pièce n°23 ?
• quelle est l’image de la pièce n°20 ?
c. Quelle remarque peux-tu faire au sujet de ces deux translations ?
d. Dans la translation qui transforme C en F :
• quelle est l’image du point D ?
• Place le point P, image de N.
• Place le point E qui a pour image N.
• Trace les quadrilatères CDHF et CENF. Quelle est leur nature ?
a. Dans la translation qui transforme A en H :• quelle est l’image de la pièce n°13 ?
• quelle est l’image de la pièce n°6 ?
• quelle est l’image de la pièce n°15 ?
• quelle est l’image de la pièce n°1 ?
b. Dans la translation qui transforme H en A :
• quelle est l’image de la pièce n°25 ?
• quelle est l’image de la pièce n°18 ?
• quelle est l’image de la pièce n°23 ?
• quelle est l’image de la pièce n°20 ?
c. Quelle remarque peux-tu faire au sujet de ces deux translations ?
d. Dans la translation qui transforme C en F :
• quelle est l’image du point D ?
• Place le point P, image de N.
• Place le point E qui a pour image N.
• Trace les quadrilatères CDHF et CENF. Quelle est leur nature ?
Exercice 2 :
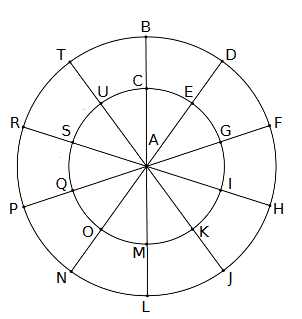
Dans cet exercice toutes les rotations sont de centre A.
H : sens horaire (sens des aiguilles d’une montre).
AH : sens anti-horaire (sens inverse des aiguilles d’une montre).
Complète le tableau suivant.
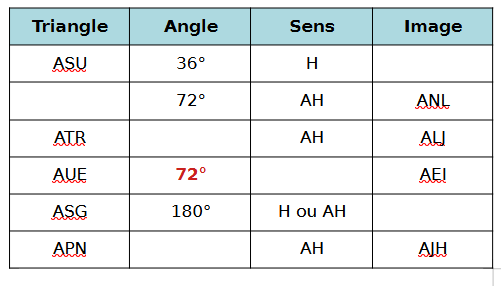
H : sens horaire (sens des aiguilles d’une montre).
AH : sens anti-horaire (sens inverse des aiguilles d’une montre).
Complète le tableau suivant.
Exercice 3 :
ABCD est un carré de centre O. Les points E, F, G et H sont les milieux des côtés du carré.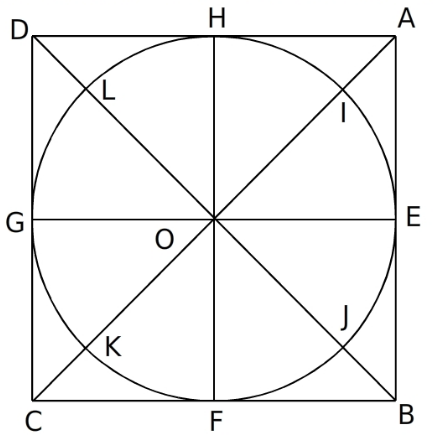 
a. Quelles sont les images respectives de A, L, G et J, par la rotation de centre O et d'angle 90° dans le sens horaire?
b. Quelles sont les images respectives de I, H, K et F, par la rotation de centre O et d'angle 45° dans le sens anti-horaire?
c. Détermine une rotation par laquelle I a pour image G.
d. Détermine une rotation par laquelle L a pour image J.
a. Quelles sont les images respectives de A, L, G et J, par la rotation de centre O et d'angle 90° dans le sens horaire? b. Quelles sont les images respectives de I, H, K et F, par la rotation de centre O et d'angle 45° dans le sens anti-horaire?
c. Détermine une rotation par laquelle I a pour image G.
d. Détermine une rotation par laquelle L a pour image J.
Exercice 4 :
Sur cette figure, ROSE est un carré de centre H. Les points I, J, K et L sont les milieux respectifs des côtés [RO], [OS], [SE] et [RE].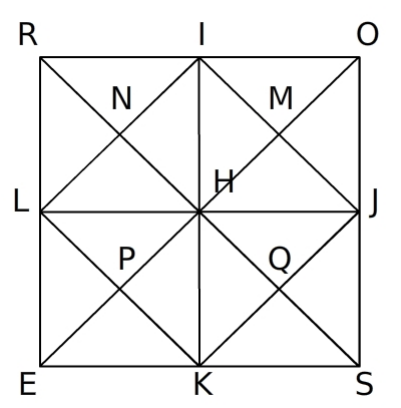 
a. Reproduis la figure en prenant RO = 8 cm.
b. Colorie en jaune le triangle RNI.
c. Colorie en rouge l'image de RNI par la rotation de centre H et d'angle 270° de sens horaire.
d. Colorie en marron l'image du triangle RNI par la translation qui transforme L en K.
e. Que dire de l'image du triangle RNI par la rotation de centre H et d'angle 360° de sens horaire ?
f. Colorie en bleu le symétrique du triangle RNI par rapport à N, puis en vert le symétrique du triangle RNI par rapport à H.
g. Colorie en violet le symétrique du triangle RNI par rapport à (LJ), puis en orange le symétrique du triangle RNI par rapport à (IK).
a. Reproduis la figure en prenant RO = 8 cm.b. Colorie en jaune le triangle RNI.
c. Colorie en rouge l'image de RNI par la rotation de centre H et d'angle 270° de sens horaire.
d. Colorie en marron l'image du triangle RNI par la translation qui transforme L en K.
e. Que dire de l'image du triangle RNI par la rotation de centre H et d'angle 360° de sens horaire ?
f. Colorie en bleu le symétrique du triangle RNI par rapport à N, puis en vert le symétrique du triangle RNI par rapport à H.
g. Colorie en violet le symétrique du triangle RNI par rapport à (LJ), puis en orange le symétrique du triangle RNI par rapport à (IK).
Exercice 5 :
Voici un pavage dont le motif de base un hexagone régulier.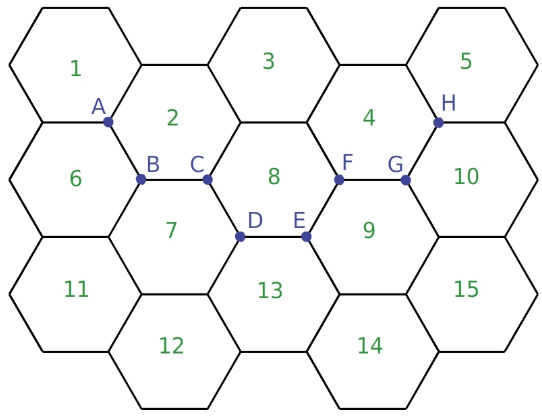 
a. Quelle est l'image de la pièce 8 par la rotation de centre C et d'angle 120° dans le sens horaire ?
b. Quelle est l'image de la pièce 9 par la translation qui transforme E en A?
c. Quelle est l'image de la pièce 15 par la translation qui transforme C en A?
d. Quel est le symétrique de la pièce 10 par rapport à (ED) ?
e. Quel est le symétrique de la pièce 13 par rapport à (GH) ? Et celui de la pièce 15 ?
f. Une pièce peut-elle avoir une autre pièce comme symétrique par rapport à un des points indiqués ? Pourquoi ?
a. Quelle est l'image de la pièce 8 par la rotation de centre C et d'angle 120° dans le sens horaire ?b. Quelle est l'image de la pièce 9 par la translation qui transforme E en A?
c. Quelle est l'image de la pièce 15 par la translation qui transforme C en A?
d. Quel est le symétrique de la pièce 10 par rapport à (ED) ?
e. Quel est le symétrique de la pièce 13 par rapport à (GH) ? Et celui de la pièce 15 ?
f. Une pièce peut-elle avoir une autre pièce comme symétrique par rapport à un des points indiqués ? Pourquoi ?
Exercice 6 :
On considère l'hexagone régulier ABCDEF.
Donner une transformation qui permet de passer :
a) du triangle OCD au triangle ODE.
b) du triangle OCD au triangle OEF.
c) du triangle OCD au triangle OCB.
d) du triangle OCD au triangle OAB.
e) du triangle OCD au triangle OFA.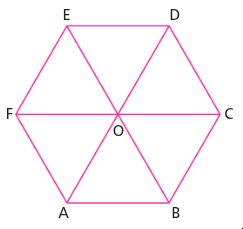
Donner une transformation qui permet de passer :
a) du triangle OCD au triangle ODE.
b) du triangle OCD au triangle OEF.
c) du triangle OCD au triangle OCB.
d) du triangle OCD au triangle OAB.
e) du triangle OCD au triangle OFA.