Chapitre 15 : Solides
Exercice 1 :
Donne le nom des solides correspondant à ces objets : 

Exercice 2 :
Complète ce tableau : 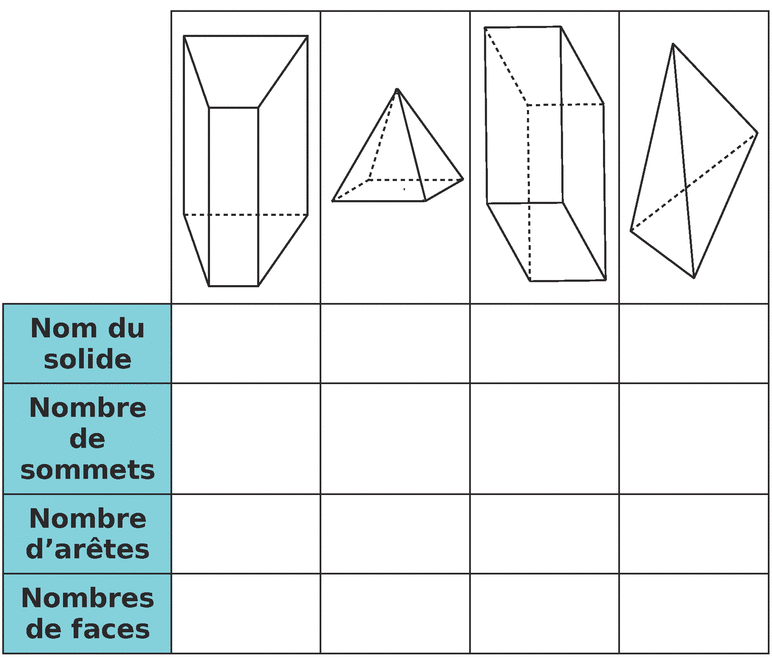 On doit à Leonhard Euler (1707-1783) la formule suivante : S + F = A + 2, où S est le nombre de sommets, F le nombre de faces et A le nombre d'arêtes. Vérifie cette formule pour les solides précédents.
On doit à Leonhard Euler (1707-1783) la formule suivante : S + F = A + 2, où S est le nombre de sommets, F le nombre de faces et A le nombre d'arêtes. Vérifie cette formule pour les solides précédents.
 On doit à Leonhard Euler (1707-1783) la formule suivante : S + F = A + 2, où S est le nombre de sommets, F le nombre de faces et A le nombre d'arêtes. Vérifie cette formule pour les solides précédents.
On doit à Leonhard Euler (1707-1783) la formule suivante : S + F = A + 2, où S est le nombre de sommets, F le nombre de faces et A le nombre d'arêtes. Vérifie cette formule pour les solides précédents.Exercice 3 :
ABCDEHFG est un polyèdre.
1. Nommer deux sommets non adjacents.
2. Nommer deux faces.
3. Nommer deux arêtes non contenues dans la même face.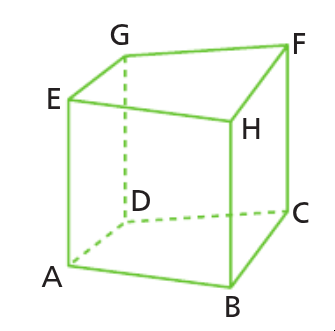
1. Nommer deux sommets non adjacents.
2. Nommer deux faces.
3. Nommer deux arêtes non contenues dans la même face.

Exercice 4 :
ABCDEHGF est un pavé droit. Donner le nombre de faces carrées et le nombre de faces rectangulaires. 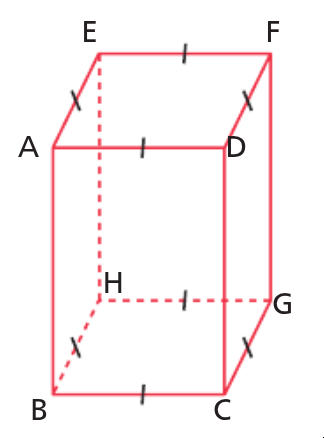

Exercice 5 :
On a représenté en perspective cavalière le prisme droit ABCDEFGHIJ.
1. Indiquer la nature du quadrilatère EFIJ.
2. Donner une arête parallèle à [FG].
3. Donner la (ou les) arête(s) parallèle(s) à [AD].
4. Donner deux arêtes perpendiculaires à [CB], puis à [EF].
5. Nommer les bases de ce prisme droit et donner leur nature.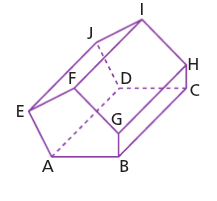
1. Indiquer la nature du quadrilatère EFIJ.
2. Donner une arête parallèle à [FG].
3. Donner la (ou les) arête(s) parallèle(s) à [AD].
4. Donner deux arêtes perpendiculaires à [CB], puis à [EF].
5. Nommer les bases de ce prisme droit et donner leur nature.

Exercice 6 :
Calcule le volume de ces pavés. 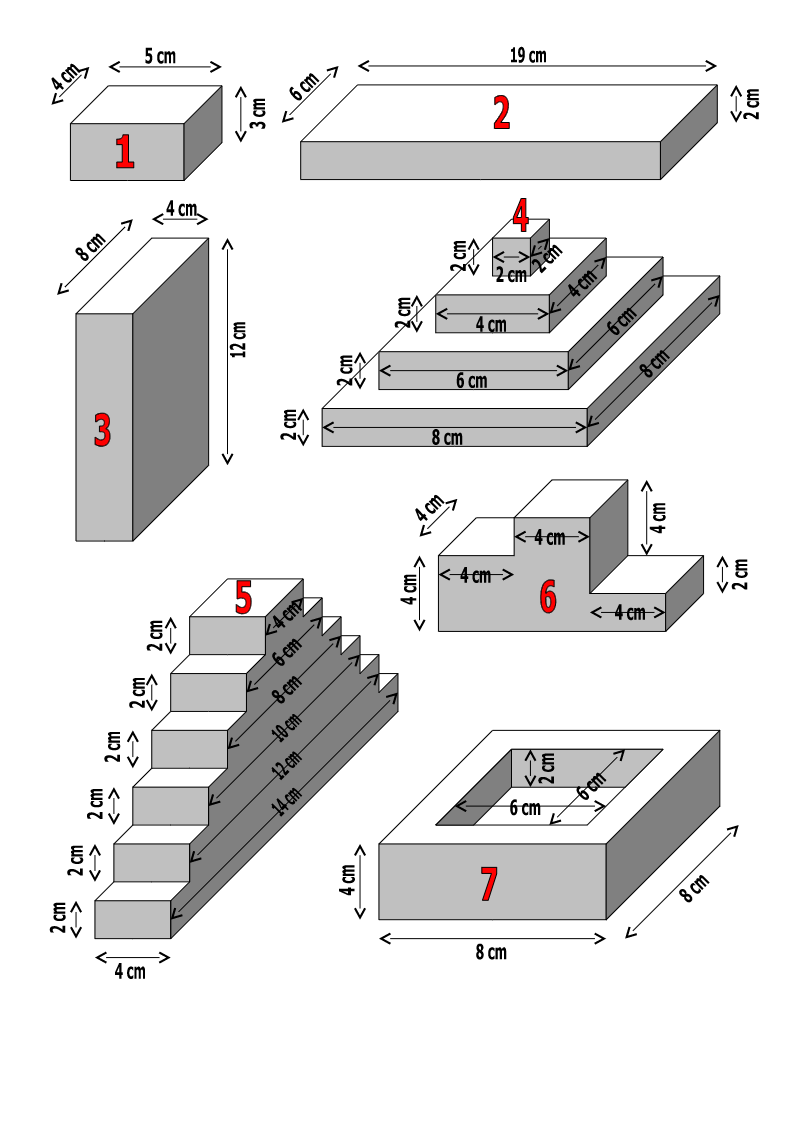

Exercice 7 :
Calcule le volume de ces prismes et de ces cylindres. Tu arrondiras à l'unité pour les cylindres. 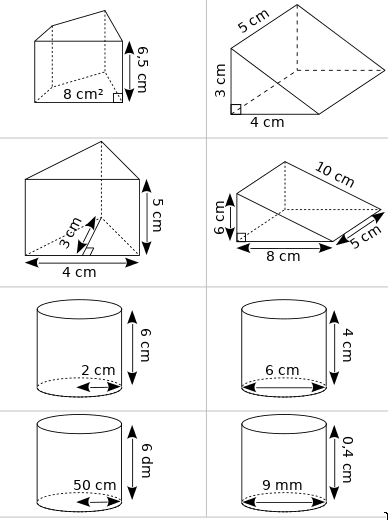

Exercice 8 :
Exercice 9 :
Pour un chantier, un maçon doit construire quatre colonnes en béton de forme cylindrique, de 50 cm de rayon et de 4 m de hauteur.
a. Quel est le volume d'une colonne (au centième de m³ près)?
b. Pour 1 m³ de béton, il faut :
Ciment : 400 kg
Sable : 460 L
Gravillons : 780 L
Eau : 200 L
Donne alors les quantités de ciment, de sable, de gravillons et d'eau nécessaires pour les quatre colonnes.
a. Quel est le volume d'une colonne (au centième de m³ près)?
b. Pour 1 m³ de béton, il faut :
Ciment : 400 kg
Sable : 460 L
Gravillons : 780 L
Eau : 200 L
Donne alors les quantités de ciment, de sable, de gravillons et d'eau nécessaires pour les quatre colonnes.
Exercice 10 :
Sram veut arroser les plantes de son jardin. Cependant, son tuyau, de 19 mm de diamètre intérieur et 25 m de long, est resté au soleil et l'eau à l'intérieur est chaude.
Ceci n'étant pas conseillé pour les plantes, Sram réfléchit au volume d'eau maximum qu'il va devoir vider avant de commencer son arrosage.
1. Recopier et compléter:
- 19 mm = ... dm;
- 25 m = ... dm.
2. Calculer alors ce volume et l'exprimer en litres.
Ceci n'étant pas conseillé pour les plantes, Sram réfléchit au volume d'eau maximum qu'il va devoir vider avant de commencer son arrosage.
1. Recopier et compléter:
- 19 mm = ... dm;
- 25 m = ... dm.
2. Calculer alors ce volume et l'exprimer en litres.