Chapitre 13 : Transformations

Définition :
Dire que deux points M et M' sont symétriques par rapport à une droite (d) signifie que la droite (d) coupe perpendiculairement le segment [MM'] en son milieu. On appelle la droite (d) l'axe de symétrie.
Exemple :
Définition :
La symétrie centrale de centre O consiste à effectuer un demi-tour autour du point O. Le point O est appelé le centre de la symétrie, il est situé au milieu de tout segment reliant un point et son symétrique.
Exemple :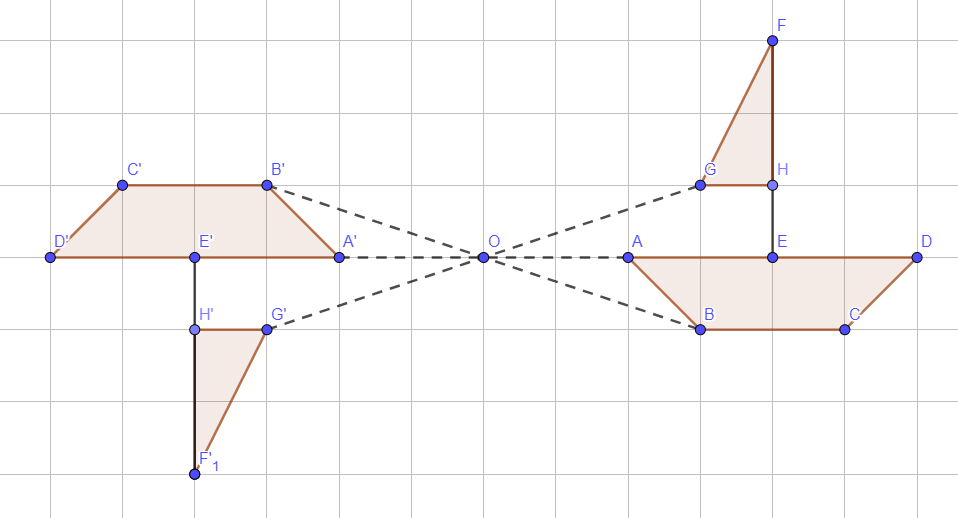
Définition :
Lorsqu'on fait glisser une figure, on applique une translation.
Exemple :
Le triangle A'B'C' est obtenue en appliquant au triangle ABC la translation qui transforme le point D en point E.
Définition :
Lorsqu'on fait tourner une figure autour d'un point d'un certain angle dans le sens horaire ou anti-horaire, on applique une rotation de centre ce point.
Exemple :
Le triangle A'B'C' est obtenue en appliquant au triangle ABC la rotation de centre O et d'angle 90° dans le sens horaire.
Remarque :
Une symétrie centrale est une rotation de 180°.
Une rotation de 90° est un quart de tour.
Une rotation de 270° est trois quarts de tour.
Une rotation de 360° est un tour entier.
Définition :
L'image d'une figure est la figure après la transformation.