02-Théorème de Pythagore - Cours
Définition :
Le carré d'un nombre est le produit de ce nombre par lui même.
La racine carrée d'un nombre positif est le nombre positif dont le carré vaut ce nombre.
La racine carrée d'un nombre positif est le nombre positif dont le carré vaut ce nombre.
Remarque :
Les racines carrées de la majorité des nombres ne sont pas décimales. Voici quelques valeurs à connaître par coeur :
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| a² | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 |
Définition :
Le côté le plus long d’un triangle rectangle est appelé hypoténuse. Il est le côté opposé à l'angle droit.
Théorème :
Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égale à la somme des carrés des longueurs des deux autres côtés. On appelle cette égalité l'égalité de Pythagore.
Exemple :
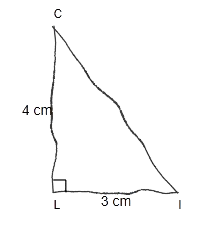Le triangle CIL est rectangle en L.Donc d'après l'égalité de Pythagore :CI² = IL² + CL²CI² = 3² + 4²CI² = 9 + 16CI² = 25CI =
Le triangle CIL est rectangle en L.Donc d'après l'égalité de Pythagore :CI² = IL² + CL²CI² = 3² + 4²CI² = 9 + 16CI² = 25CI =
Exemple :
.png)
Le triangle BAR est rectangle en A. D'après l'égalité de Pythagore :BA²+AR²=BR²BA²+16²=19²BA²+256=361BA²=361-256BA²=115BA =
Le triangle BAR est rectangle en A. D'après l'égalité de Pythagore :BA²+AR²=BR²BA²+16²=19²BA²+256=361BA²=361-256BA²=115BA =